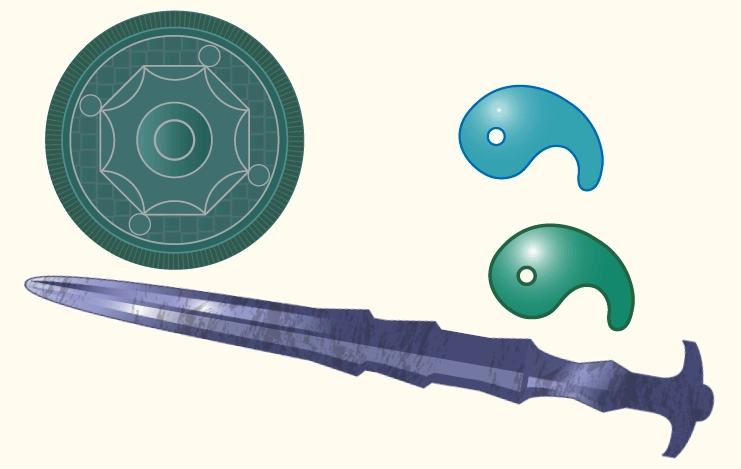
2進数 "11111111" は10進数では "255" ではあるんですが、プログラマー用の電卓では "-1" が出てびっくりすることがあります。
2進数整数のマイナス表現は意外とつまづくところです。でもこれから説明するものだけ理解できれば大丈夫。
2進数 \( 11111111 = -1\) は決して間違いじゃありません。これも正解です。"255" と "-1" 、ぜんぜんちがう値ですが、2進数では同じ値。
これが分かる人、そして上の文章ではある条件が抜けてるために、まちがった文章になっていることに気づく人は、2進整数について言うことはありません。ここから先読まなくていいです。
2進の整数は意外と知らなきゃいけないことがあるので、今回は小数のことには触れません。小数点は固定少数や浮動小数の話もありさらに複雑になるから。
一番左は符号ビット
まずはこのルールから行きましょう。"11111111" の一番左の "1" は符号ビットです。
| 0 | 正(+) |
| 1 | 負(-) |
残りの7ビットが絶対値(数字部分)。
サイズは8bit(1byte)なんですが、絶対値の表現できる範囲は7bit分の0~128で、整数の表現範囲は-128~127です。
| 26 (64) | 25 (32) | 24 (16) | 23 (8) | 22 (4) | 21 (2) | 20 (1) |
\(64 + 32 + 16 + 8 + 4 + 2 + 1 = 127\) (に0を足して128通り)。マイナス分を足して256通り。
正の整数を明示すれば 11111111 は 255
『一番左の符号ビットを数字で使う』と明示すれば符号ビットはなくなり、8bit分すべてを正の整数に使えて2進数11111111 = 255 になります。
たとえば、C, C++言語の型ではこうなる。
| char | -128~127 |
| unsigned char | 0~255 |
char型は1byte(8bit) サイズの変数で、unsignedは符号ビットなしを指定します。(un + signed : サイン(+, -)をun(否定)する。)
冒頭の文章が言葉足らずで間違っているというのはここ。『符号なし』『正の整数を明示』の条件が抜けていました。
サイズを変えてもいいが 011111111 と 11111111 はちがう。
もうひとつ、符号ビットを9桁目以降にしてサイズを変える方法もありますが注意が必要です。"11111111" は間違いになる。
人間が使う10進数では、"10" を "0010", "00000010" などと書かないですが、2進数では必ず有効桁数で書きます。(左は0詰め。)
たとえば倍の16bit(2byte)に変えた場合、"0000000011111111" になり符号ビットが0になって値は255。
電卓を使えば『\(11111111 = -1\)』『\(0000000011111111 = 255\)』になってすぐに分かるはず。
ちなみに整数値の有効桁は、1, 2, 4, 8, 16, 32, 64, 128, ...を使い、9とか10など中途半端なものは使いません。
コンピュータは2の累乗でブロックを作って処理をするので都合がいい。
『32ビットCPU』『64ビットCPU』など言われるが、この数値の部分が処理するブロックの単位。
32ビットアーキテクチャ、64ビットアーキテクチャという。
(アーキテクチャ(構造)はCPUの仕組み、仕様のこと。)
昔は処理能力が低く、4ビット、8ビット、16ビットのアーキテクチャがあった。
そこまで高い能力を必要としない組み込み系のマイコンでは今でも使われる。
マイナス値の数字は10進数は大きくなるけど2進数は小さくなる
10進数ではマイナス値が小さくなるほど絶対値(数字部分)が大きくなりますが、2進数は逆で-1の絶対値が "1111111" で-128が"0000000"になります。
| -1 | 11111111 |
| -2 | 11111110 |
| -4 | 11111100 |
| -8 | 11111000 |
| -16 | 11110000 |
| -32 | 11100000 |
| -64 | 11000000 |
| -128 | 10000000 |
絶対値の並びを逆転したときのルール
ここで符号のことは忘れましょう。絶対値(数字部分)だけを見ます。さっきの表から符号を取ります。
| 10進 の値 | 2進 の値 | 2進値を10 進に変換 |
|---|---|---|
| 1 | 1111111 | 127 |
| 2 | 1111110 | 126 |
| 4 | 1111100 | 124 |
| 8 | 1111000 | 120 |
| 16 | 1110000 | 112 |
| 32 | 1100000 | 96 |
| 64 | 1000000 | 64 |
| 128 | 0000000 | 0 |
2進数のマイナスの絶対値は、10進数の絶対値を足すと128になる値です。
128 = (10進の絶対値)+(2進の絶対値)
ここで疑問が。2進数表現のマイナス値をビット配列から見るとき、 有効桁で表現できる絶対値の数(ここでは128通り)を知らないと分からないのか? ということ。
この128を知らずに見ることができるのが2の補数。
2進数の絶対値の逆転(2の補数)
今度は絶対値の逆転をすべて2進数で見てみましょう。
| 10進の値を 2進に変換 | 2進 の値 |
|---|---|
| 0000001(1) | 1111111(127) |
| 0000010(2) | 1111110(126) |
| 0000100(4) | 1111100(124) |
| 0001000(8) | 1111000(120) |
| 0010000(16) | 1110000(112) |
| 0100000(32) | 1100000(96) |
| 1000000(64) | 1000000(64) |
| 10000000(128) | 0000000(0) |
ここで登場するのが2の補数です。補数はこれだけでもけっこうな内容になるのでここでは割愛します。
2の補数は『0と1を交代して+1』。これを表に加えます。
| 10進の値を 2進に変換 | 2進 の値 | 2進値の 2の補数 |
|---|---|---|
| 0000001(1) | 1111111(127) | 0000000 + 0000001 |
| 0000010(2) | 1111110(126) | 0000001 + 0000001 |
| 0000100(4) | 1111100(124) | 0000011 + 0000001 |
| 0001000(8) | 1111000(120) | 0000111 + 0000001 |
| 0010000(16) | 1110000(112) | 0001111 + 0000001 |
| 0100000(32) | 1100000(96) | 0011111 + 0000001 |
| 1000000(64) | 1000000(64) | 0111111 + 0000001 |
| 10000000(128) | 0000000(0) | 1111111 + 0000001 |
2進数の絶対値の2の補数を10進数に変換してマイナス(-)を付けるとマイナス値の2進数 -> 10進数変換の完成です。
なぜマイナス値は、2進数と10進数で数字の大小が逆転するのか?
数値で数が大きくなるにはひとつの性質があります。右にずらし(シフト)たら位が上がって大きくなり、左にシフトしたら位が下がって小さくなるというもの。
10進数なら10を掛けて位を上げる、2進数なら2を掛けて位を上げると同じ意味です。
(位が下がるには10進数なら 1/10, 2進数なら1/2を掛ける。)
| 1 |
| 10 |
| 100 |
| 1000 |
左にシフトしたときは右に0を詰めます。次は2進数のさっきの表から見てみましょう。
| 1111111(127) |
| 1111110(126) |
| 1111100(124) |
| 1111000(120) |
| 1110000(112) |
| 1100000(96) |
| 1000000(64) |
| 0000000(0) |
色が付いたところが同じように変化していることが分かります。最後の "0000000" は "10000000" の0詰めの部分。2進数は数字を入れるサイズが決められているので(ここでは7桁)、1が消えました。
ずらしたあと空いたところに符号ビットを詰める
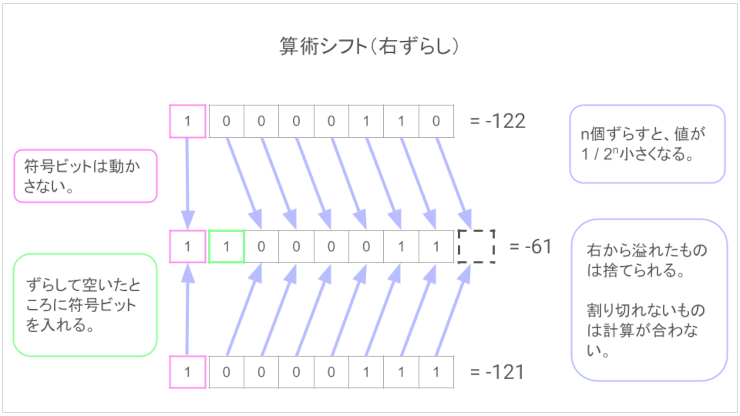
2進数では、マイナスの整数は右にシフト(1/2 ずつ小さくする。位を下げる)すると左に1を詰めるというルールがあります。
そのルールを考えるとマイナスの整数のスタート(-1)は1並びになる。これが『-1が1並び』の正体でマイナス値が小さくなれば絶対値も小さくなる正体。
右シフトで左に符号ビット詰め、左シフトで右に0詰めのことを算術シフトといいます。掛け算・割り算で使う。
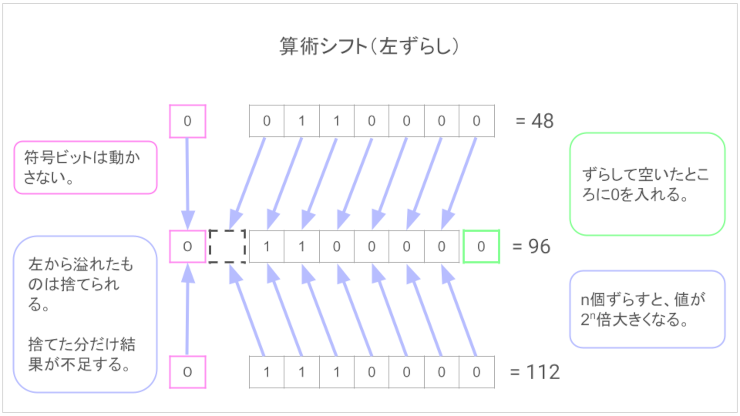
右シフト、左シフトともに0詰めするシンプルなのを論理シフトといい、算術シフト・論理シフトの2つのことをシフト演算という。
論理シフトのほうが符号ビットがない分、表現範囲が広いが、掛け算・割り算では算術シフトを使う。
(あまり知られないところで論理シフトも使うのかもしれないが。)
はみ出した値はどうなる?
-128は、左シフトの結果 "10000000" の0の部分と言いましたが、1はどこへ行ったのでしょうか?
答えは、もう言いましたが捨てられておしまい。
整数の表現では値が決まっているので、切り捨ての結果だろうがなんだろうが関係ないですが、足し算・引き算・掛け算・割り算の算術計算、値の代入では問題になります。
この問題を『オーバーフロー』(桁あふれ)と言います。
1byte(8bit)の箱(変数)に表現範囲外の128や-129を入れようとしたり、1byteの整数同士の掛け算の結果を1byteの変数に入れると、表現範囲外の結果になれば値の一部が切り捨てられるので計算が狂います。
値の代入や計算結果の変数では、あらかじめ余裕のある最大桁数、表現範囲を決める必要があります。それから漏れる値(オーバーフロー)はエラーとして処理するなどが必要。
整数を入れる変数(int)の標準的なサイズは4byte(32bit)で、表現範囲は-2,147,483,648~2,147,483,647。
(約、プラマイ21億)
システム上かなり余裕があるので、そのまま使っても良い。
なんでこんな面倒なことした?
2進数のマイナス整数値では、絶対値を大から小へ10進数と逆転させたり、算術シフトの右シフトで符号ビットを詰めたり、面倒なことをいろいろしています。
その理由を見聞きしたことはないんですが、ひとつでも表現範囲を広げるためにしたんじゃないだろうか?
たとえば、-1を "10000001" にした場合、"11111111" は-127になります。これだと-128は入れられません。
今となってはどうでもいい話ですが、性能が低いコンピュータを効率よく動かすために、できるだけ表現範囲を広めた必死の努力の結果に見えます。
数学の強者たちが考えた方法なので他にも理由がありそう。ザ・凡人には想像もつきませんが。
シンプルな方法に変えようにも、もうできないでしょう。今ルールを変更してしまうと世界中のコンピュータの計算が狂ってしまうので。