コンピュータの基礎知識では補数(ほすう)が出てきます。ここでつまずいて嫌になる人もいるくらい。
『つまずくなら式を覚えてしまえ』でスルーしてもいいですが、メカニズムを分かってないとすぐに忘れます。
『試験以外で使ったことないからいい』という意見を否定しませんが。
補数はコンピューターの基礎知識でつまずきやすい上位にくるところ。かく言うボクもとりあえず試験対策用に覚えたタイプ。メカニズムまで人に説明できるレベルじゃありませんでした。
今回これを書くに当たり、多くの人に分かってもらうためにはどうしたらいいか考えました。メカニズムのそもそも論が多すぎてまとめにくいから。
正直、自己採点での出来はいまいちです。そして、シチューの次の日にカレーライスが出てきたくらい、なんとも重い内容。
(『文句を言うならお前が作れ!』はナシで。思うだけで口には出しません。殺されるから。)
なので最初にポイントから。
2進数の基数の補数(2の補数)
コンピュータは引き算ができないため、足し算で引き算をするのに使う。
引く値の補数を足すだけで済む。
\[X - Y = X + (Yの補数)\]
2進数の減基数の補数(1の補数)
"2の補数" を作るのに使うビット列の反転のこと。それ以外に使いみちはない。
10進数の基数の補数(10の補数)
引き算の桁下がりで使う。小学校で習ってる。
同じ桁同士の計算でしか使わない。
10進数の減基数の補数(9の補数)
使いみちは... 知らん。
減基数の補数
\[(減基数の補数)=(基数の補数) -1\]
何進数だろうが同じ。
俗に、10進数なら『9の補数』、2進数なら『1の補数』という。
これについていろいろ話をしていきます。
補数とは何か?
補数というと最初に出てくるのは、10進数では『足して10になるもの(足して上の位になるもの)』。
\begin{array}{lclcr}
6の補数&\rightarrow&10-6&=&\underline{4}\\
83の補数&\rightarrow&100 - 83& =& \underline{27}
\end{array}
2進数では、『反転して+1』『1の補数+1』(くわしくはあとで)と説明がされますが、分かりやすい言葉を使えば、『計算を簡単にするために元の値から算出される特殊な値』のことを言います。
確かに10進数や2進数の補数は上のルールで覚えても良いんですが、補数の算出の方法や使いどころ、性格がそれぞれあるので覚えづらいです。
必死に覚えようとすればするほどつまずきやすいので、まず最初は『簡単に計算するための値』とシンプルに考えましょう。
そろばんの補数
補数にはいろいろあるという例としてそろばんがあります。
一番オーソドックスなそろばん(独立した玉が上にひとつ、残りの4つが縦に並んだもの)には、玉を速く動かす補数があります。
| 桁上がり の足し算 | 桁下がり の引き算 | ||
|---|---|---|---|
| 1の補数 | -4 | -1の補数 | 4 |
| 2の補数 | -3 | -2の補数 | 3 |
| 3の補数 | -2 | -3の補数 | 2 |
| 4の補数 | -1 | -4の補数 | 1 |
| 5の補数 | 0 | -5の補数 | 0 |
なんのことか分からないですよね? 桁上りの足し算、桁下がりの引き算で使う補数です。
そろばんで6+4をするとき単純に4を足せません。そのとき、
上の玉を上に弾く(-5)
下の4玉のひとつを下に弾く(-1。桁上りの4の補数)
ひとつ上の位の4玉のひとつを上に弾く。(+10)
という作業をします。
(ここはそろばんの勉強ではないのでくわしくは割愛)
\[6+4 = 6 +(-5 \textcolor{#cf2e2e}{-1} + 10)\]
計算式自体は合っているので、そろばん以外でも使えますが、脳内でそろばんの玉をイメージできないと逆に補数が計算を複雑にしてしまいます。
(玉を脳内でイメージできる人には爆速計算。)
『補数はこうするんだ!』に囚われずケースバイケースで見ましょう。
補数の覚え方
まず、何のための補数か考える。
『〇〇の計算を簡単にする方法があったな?』
『そのとき〇〇の補数を使うな。』
ぐらいの感覚でいい。どこで?何を?が重要。
いきなり方法から入ると覚えにくい。
使いどころをまちがえると、とんでもないことも起きる。
あとで説明しますが、10進数の56-123を、123の補数で計算すると答えが正しく出ません。10進数の引き算で使う補数の使い方がまちがっているから。
10の補数(基数の補数)の使う場所は、同じ桁同士の引き算。
ね? 使う目的、場所は大事ですよ? の典型的な例です。
補数にはふたつの種類がある。
補数は『数値をひとつ上の位から引いた値』です。言い換えると、『数値とその補数を足すとひとつ位が上がって切りが良い』。
\begin{array}{c}
83の補数 \\[+10px]
100 - 83 = \textcolor{#cf2e2e}{27}
\end{array}
〇〇進数の『〇〇の補数』
上記の補数のことを『10の補数』と言います。これが2進数なら『2の補数』と言います。
たんに『補数』と呼ばれるのもこれ。
また、〇〇進数の〇〇は基数なので『基数の補数』ともいいます。
ただ、『10の補数』は名称なのか、10進数の『90』なのか、イチ・ゼロと読んで2進数の『110』なのか区別がつきません。
『10の補数』『2の補数』は通称だと見たほうが良いです。たんに補数というか正確に『基数の補数』と言いましょう。
減基数の補数。『(〇〇-1)の補数』
補数にはもうひとつあります。『位が上がらない最大値から引く補数』。言葉にすればややこしいですが、さっきの例で言えば、
\begin{array}{c}
83の減基数の補数 \\[+10px]
99 - 83 = \textcolor{#cf2e2e}{26}
\end{array}
10進数なら『9の補数』、2進数なら『1の補数』とも言われます。言葉ではなんのこっちゃですが、補数(基数の補数)から-1したもの。
『ふたつの補数を知ったところで、どうした? 使いみちは?』と思ってしまうところが補数の弱点であり、覚えにくいところですが、補数は小学校の算数ですでに使っています。気づいていないだけで。
小学校の算数で使われている補数
ここで小学生に戻ってみましょう。いつ習ったのかすら覚えてないほど子供のころに習った引き算をします。
(1) 一の位の計算
\begin{array}{r}
\textcolor{#cf2e2e}{1}\phantom{000} \\[-3px]
1\cancel{2}3\phantom{0.} \\[-3px]
\underline{-\phantom{00}5\cancel{6}\textcolor{#cf2e2e}{4}}\\[-3px]
7\phantom{0.} \\[15px]
\end{array}
\(3-6\) ができないので、十の位の2から10を借りてきて、\(10-6\) をする。10を貸した2から1を引く。
引き算が終わったので、残りの3と4を足す。
\[\underline{3+4 = 7} \cdots 一の位\]
(2) 十の位の計算
\begin{array}{r}
\textcolor{#cf2e2e}{0\phantom{0}1}\phantom{0000.} \\[-3px]
\cancel{1}\cancel{2}\phantom{0.}3\phantom{0.} \\[-3px]
\underline{-\phantom{00}\cancel{5}\textcolor{#cf2e2e}{5}\cancel{6}\textcolor{#cf2e2e}{4}}\\[-3px]
6\phantom{00}7\phantom{0.} \\[15px]
\end{array}
\(1-5\) ができないので、百の位の1から10を借りてきて、\(10-5\) をする。10を貸した1から1を引く。
引き算が終わったので、残りの1と5を足す。
\[\underline{1+5 =6} \cdots 十の位\]
\[\underline{答え\phantom{0}60+7 = 67}\]
小学校の引き算はそのまま補数でできる
これ、頻繁に補数を使ってるのに気づいているでしょうか?同じことを補数という言葉を使って表現します。
(1) 一の位の計算
\begin{array}{r}
\textcolor{#cf2e2e}{1}\phantom{000} \\[-3px]
1\cancel{2}3\phantom{0.} \\[-3px]
\underline{-\phantom{00}5\cancel{6}\textcolor{#cf2e2e}{4}}\\[-3px]
7\phantom{0.} \\[15px]
\end{array}
\(3-6\) ができないので、6の補数を出して引かずに足す。
\[\underline{3\textcolor{#cf2e2e}{+4} = 7} \cdots 一の位\]
補数を出すときに十の位から10を借りているので、十の位から1を引く。
(2) 十の位の計算
\begin{array}{r}
\textcolor{#cf2e2e}{0\phantom{0}1}\phantom{0000.} \\[-3px]
\cancel{1}\cancel{2}\phantom{0.}3\phantom{0.} \\[-3px]
\underline{-\phantom{00}\cancel{5}\textcolor{#cf2e2e}{5}\cancel{6}\textcolor{#cf2e2e}{4}}\\[-3px]
6\phantom{00}7\phantom{0.} \\[15px]
\end{array}
\(1-5\) ができないので、5の補数を出して引かずに足す。
\[\underline{1\textcolor{#cf2e2e}{+5} =6} \cdots 十の位\]
補数を出すときに百の位から10を借りているので、百の位から1を引く。
\[\underline{答え\phantom{0}60+7 = 67}\]
ここで補数の特長が出ました。引くほうを補数にすると引き算が足し算に変わります。
1個の補数を使って引き算を足し算にする
上記では位ごとに補数を使いましたが、引く値をまるごと補数にしてから1回の足し算で引き算をしてみましょう。
\[123-56\]
(1) 補数を出す
56の補数を出す。ここでは123の3桁に+1した4桁の1000を使う。
\[1000 - 56 = 944\]
(2) 補数を使って足し算
\begin{array}{r}
123 \\[-3px]
\underline{+\phantom{00}944}\\[-3px]
\textcolor{#cf2e2e}{\cancel{1}0}67 \\[15px]
\end{array}
足し算の有効桁は3桁なので1000は切り捨て。また結果の0はいらない。
一見、ちゃんとできているように見えますが、10進数でこれをすると都合が悪いです。今度は小さい値から大きい値を引いてみましょう。答えを先にいうと正しい値になりません。
\begin{array}{l}
123の補数\\
1000 - 123 = 877
\end{array}
\begin{array}{r}
56 \\[-3px]
\underline{+\phantom{00}877}\\[-3px]
933 \\[15px]
\end{array}
10進数の補数は位ごとに出して使う分には良いが、1回でする分には都合が悪い。
コンピュータは引き算ができない
さっきの10進数での例では引き算を使いました。これ小学校の引き算で補数を使っているから出したんじゃありません。
2進数の引き算で万能感を発揮するのが『基数の補数』(2の補数)だからです。
じつはコンピューターは頭が良いようですこぶる悪いです。そもそも0と1以外の文字を認識できない。その0と1でさえ電気を流したときのスイッチのON/OFFみたいなもの。
そんなコンピューターの計算では小学校レベルの引き算すらそのままではできません。そこで登場するのが2進数の基数の補数です。
2進数では、引く方の値を丸ごと補数に変えて補数を足すと、引き算とまったく同じ結果になります。
\begin{array}{rcl}
X-Y &=&X +(Yの補数)
\end{array}
2進数の補数はコンピューターができない引き算を足し算に変えるのに使う。
2進数の引き算(補数での足し算)
さっそく補数の足し算をして引き算と同じ結果が出るのか見ていきましょう。
\begin{array}{lcrcr}
123 - 56 =67\\
123の2進数&\rightarrow&1111011&\rightarrow&01111011 \\
56の2進数&\rightarrow&111000&\rightarrow&00111000\\
56の補数&\phantom{0}&\phantom{0}&\rightarrow&11001000
\end{array}
\begin{array}{r}
01111011 \\[-3px]
\underline{+\phantom{0}11001000}\\[-3px]
01000011
\end{array}
\[\underline{01000011の10進数\rightarrow67}\]
正しく答えが出ましたね? でも気になるところがあります。
123と56の2進数の左になんで0を付けたの?
2進数の補数を出すの難しくね?
足し算が間違ってるでしょ?
これを解説します。
2進数の補数は図で見ると分かるが、数式では凡人には理解不能
2進数の補数(基数の補数(2の補数))は『反転して+1』です。このしくみはあとで分かるので置いといて、その基本になるのが、整数のマイナス値の作り方。
10進数のマイナス値は値が小さくなれば絶対値は大きくなりますが、2進数では絶対値は大きくなります。
ここでいう2進数の絶対値は0と1のビット列のこと。
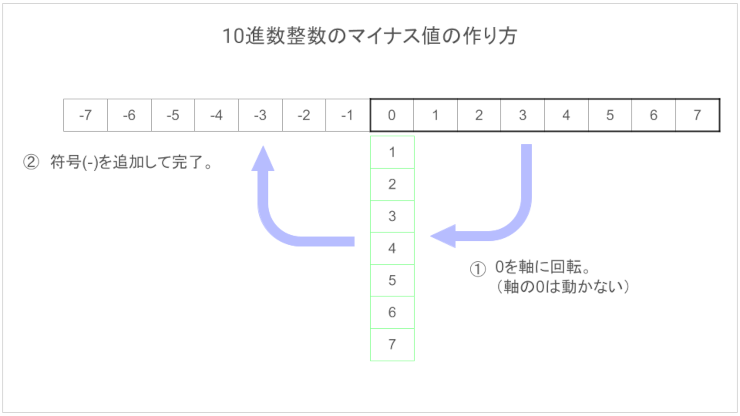
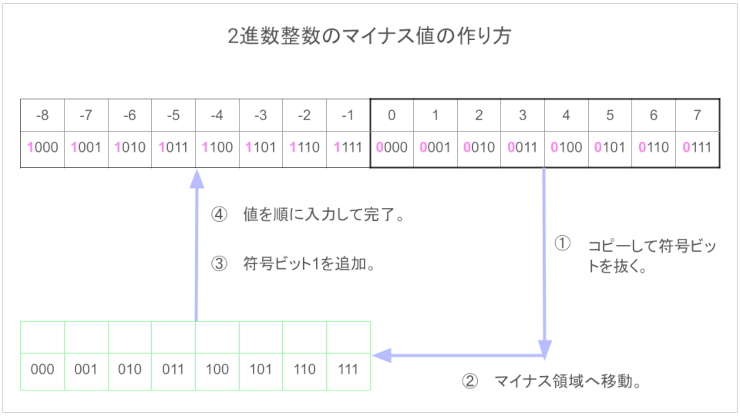
絶対値のビット列の大小を逆転してマイナス値を表現します。当然、コンピューターは10進数に変換すると帳尻を合わせてくれます。
そうなるとマイナス値はよく見る2進数→10進数の変換ができないことに注意。
\begin{array}{rcl}
0101 &=& (2^2\times1) + (2^1\times0) + (2^0\times1)\\
&=& 4 + 1\\
&=& 5
\end{array}
こういう式は成り立ちません。試しに図の-4の2進数を同じようにしてみましょう。
\begin{array}{rcl}
1100 &=& (2^3\times1)+(2^2\times1) + (2^1\times0) + (2^0\times0)\\
&=& 8+4\\
&=& 12
\end{array}
当たり前です。作りがちがうんだから。それ以外にも算術シフトがあったりしてもう少し変わったビット列を持ちます。
補数(2の補数)= 『反転して+1』の正体
補数を出す方法の『反転して+1』を知るには、まず図を見たほうが速いです。
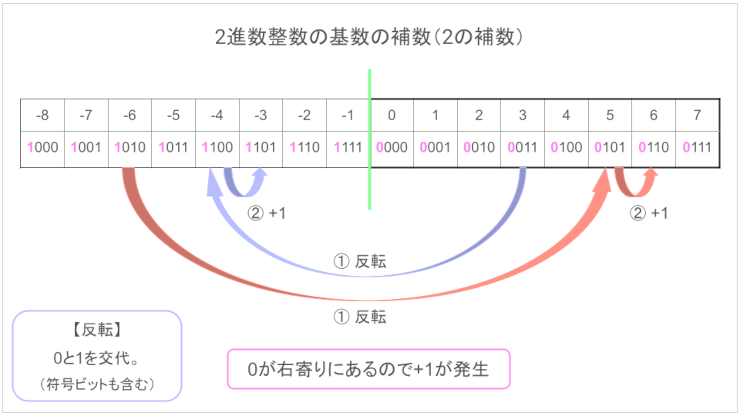
2の補数はコンピューターが引き算を足し算でやってしまうためにあると言いました。さっき出た数式をもう一度見てみましょう。
\begin{array}{rcl}
X-Y &=&X + (Yの補数)
\end{array}
2進数の値を10進数にして見ると小学生でも分かります。
| 1の補数 | -1 |
| 2の補数 | -2 |
| 3の補数 | -3 |
| -1の補数 | 1 |
| -2の補数 | 2 |
| -3の補数 | 3 |
2進数の補数は符号が変わるだけ。これが2進数ではシンプルに引き算を足し算にできる正体です。
さっきのXYの式に適当に値を入れてみましょう。Y = 285 にしてみます。
\begin{array}{rcl}
X-Y &=&X + (Yの補数)\\
X-285 &=&X + (-285)\\
\end{array}
説明するまでもないですね? これを2進数ですると『反転して+1』になる。ビット列のこの現象は、数学の凡人には説明できません。
凡人にも分かることは、プラス値に符号ビット0を入れるのは反転だけで符号を変えるため。
+1は符号を抜いたビット配列の0だけ並びを、ゼロ以外にマイナスの最小値にも使ってて、その分ズレた修正を+1でしていることくらい。
だからボクの説明も図を最初に見せました。
符号ビットも含めて反転させる。そうしないと符号が変わらない。
もちろん、プラスの符号ビットは必ず付ける。省略できない。
2進数の補数は10進数に変換して見ると符号が変わるだけ。
\[〇〇 = -(〇〇の補数)\]
2進数と10進数の大きな違いは、絶対値0をどう使うか?
10進数の絶対値0はプラスとマイナスの境界線で符号は付かない。
2進数は絶対値0にプラスとマイナスの符号をつけて、プラス0は10進数の0を、マイナス0はマイナスの最小値を表現する。
そもそも10進数のゼロに符号はないので絶対値0という概念はないと思うが。
| プラス0 | マイナス0 | |
|---|---|---|
| 10進数 | 便宜上+0の表現はあるが、 正確には0に符号はない。 (ゼロはゼロ。) | 左に同じ。 |
| 2進数 | 正の符号(0)を付けて、 10進数のゼロを意味する。 (0000) | 負の符号(1)を付けて、 表現できるマイナス値の 最小値を意味する。 (1000) |
『反転』と+1の順序は守ろう!
よくありがちなのが、『反転して+1』のうろ覚えで+1を先にやってしまうこと。これはまちがい。もう一回、図を見てみましょう。

2進数の絶対値のビット列は、プラス領域で+1すると外に向かって動きますが、マイナス領域で+1すると内に向かって動きます。
反転は狙ったところに飛ばす役割なので、反転の前に1ずらすと着地も1ずれる。
(反転は符号ビットが変わるところ(図の緑線)を軸にして等距離の場所へ飛ばす。)
たとえば、図の青矢印で言えば、反転の前に+1して(0100)飛ばすと、1011に着地する。-3が-5になります。
『反転した後に+1』は絶対です。
2進数の基数の補数(2の補数)= 反転して+1
補数をかんたんに出すために使う減基数の補数
冒頭で出てきてまだ使ってない補数があります。減基数の補数です。2進数では0と1を反転させるだけで出せる。信じられない人のために証明していきましょう。
まず、10進数で減基数の補数を考えます。10進数では『足して9になる』もの。
\begin{array}{rcl}
9の補数&\rightarrow&0\\
7の補数&\rightarrow&2\\
4の補数&\rightarrow&5\\
\end{array}
2進数では『足して1になる』もの。
\begin{array}{rcl}
0の補数&\rightarrow&1\\
1の補数&\rightarrow&0\\
\end{array}
2進数では0と1しか使えないので反転するだけ。2進数の減基数の補数(1の補数)は反転を意味します。
2進数はスイッチのON / OFF みたいなものと言ってるのはこういうこと。
ON の反対は OFF
OFF の反対は ON
これが反転の正体。
ここで減基数の補数の性格を思い出しましょう。
\begin{array}{rcl}
(補数)&=&(減基数の補数)+1\\
&=&(反転)+1
\end{array}
さっき+1はズレを直すためと言いましたが、補数と減基数の関係がそれを表現しています。
2進数では『足して2になる値』で補数を作るのは難しいです。こっちのほうが簡単。
2進数の減基数の補数(1の補数)は基数の補数を作るとき以外には使いません。
足し算であふれたものは切り捨て
『反転して+1』のボリュームが多すぎてひとつ忘れるところでした。
もう1回、頭の計算に戻りましょう。
\begin{array}{lcl}
123 - 56 =67\\
123の2進数&\rightarrow&01111011 \\
56の2進数&\rightarrow&00111000\\
56の補数&\rightarrow&11001000
\end{array}
\begin{array}{r}
01111011 \\[-3px]
\underline{+\phantom{0}11001000}\\[-3px]
01000011
\end{array}
ただこの足し算まちがってます。本当ならこうなるはず。
\begin{array}{r}
\textcolor{#cf2e2e}{1111}\phantom{0000} \\[-3px]
01111011 \\[-3px]
\underline{+\phantom{0}11001000}\\[-3px]
\textcolor{#cf2e2e}{1}01000011
\end{array}
でもコンピュータの計算は間違いじゃありません。2進数は有効桁が決まっているのであふれる1は切り捨てられます。
足し算に符号ビットも入れる
足し算でもう一つ疑問が。『符号ビットも計算に入れるの?』ということ。
答えは『Yes』です。
2進数の引き算では、符号ビットも足し算に入れるから計算できるようになっています。\(56-123 = -67\)でやってみましょうか?
10進数ではできなかったリベンジです。
\begin{array}{lcl}
56-123 =-67\\
56の2進数&\rightarrow&00111000\\
123の2進数&\rightarrow&01111011 \\
123の補数&\rightarrow&10000101
\end{array}
\begin{array}{r}
00111000 \\[-3px]
\underline{+\phantom{0}10000101}\\[-3px]
10111101
\end{array}
これを10進数に変換して答え合わせしましょう。マイナス値の2進数→10進数の変換も『反転して+1』です。くわしくは別に書いたのでここは計算だけ。
(ややこしいのか、覚えることが1個でラッキーなのか複雑な気分になるが。)
\begin{array}{rclcl}
10111101&\rightarrow&(反転)&\rightarrow&01000010\\
&\rightarrow&(+1)&\rightarrow&01000010+00000001=01000011
\end{array}
\begin{array}{rcl}
01000011 &=& 2^6\times1+2^1\times1+2^0\times1\\[-3px]
&=&64+2+1=67
\end{array}
最後に符号を付けて、\(\underline{-67}\)
2進数やその補数がスゴいところは、ビット配列をいろいろ工夫して計算をかんたんにしているところ。
引き算を足し算でできるようにビット配列を工夫したとも言える。
メカニズムを知るとスゲ~の一言。すべてを説明できないので余計に
2進数の補数(2の補数)は反転 + 1 で出す。
マイナスの2進数値を10進数に変換するときも反転 + 1 で出す。
偶然そうなったのか、覚えやすいとかの意図があるのかは凡人には分からない。
数学的な正しさ・美しさがあるのだろう。












