2進数から10進数へ変換したあと、元に戻そうと10進数から2進数へ変換したら値が変わってしまう現象が起きます。
これは変換のルールだけ知っていても正しい変換ができないから。
『10進数と2進数では絶対値の考え方がちがう』ところが抜けてるよ?という話です。
まずは10進数の9を2進数に変換するところを見てください。
\begin{array}{l}
9&=\\
&=8+1\\
&=2^3\times\textcolor{#cf2e2e}{1}+2^2\times\textcolor{#cf2e2e}{0}+2^1\times\textcolor{#cf2e2e}{0}+2^0\times\textcolor{#cf2e2e}{1}\\
\phantom{0}&\rightarrow01001
\end{array}
2進数では符号(+,-)が省略できないので符号ビット(0:+)を左に付けます。
今度は、-9を2進数に変換してみましょう。符号ビットを変えて "11001" にしたいところです。でもこれがまちがい。
正解は "10111" になります。符号ビットを除いた絶対値を10進数に変換すると7になります。
ぜんぜんちがう。この現象はマイナスの整数だけで起きます。2進数整数のマイナス値ではもう一味、加えられているから。うどんにかける一味みたいなスパイスが。
なぜマイナス値は一味ちがうのか?
マイナス値の整数が一味ちがうのは整数の考え方がちょっとちがうから。具体的には算術シフトを使っているからです。
まず10進数で整数の性格を見てみましょう。整数は、数字の並びを右にシフトすると1/10, 1/100, ... と値が小さくなり、左にシフトすると10倍, 100倍, ... と値が大きくなります。
0を右に付ける、右の0を取るだけで瞬時に倍数の計算ができる仕組み。小学校で習って無意識にできることなので考えたこともないでしょう。
これは2進数でも言えます。ただ倍数の増え方、減り方がちがうだけ。〇〇進数の基数を使うと一目瞭然。
| 10進数 | ... | 104 (10000) | 103 (1000) | 102 (100) | 101 (10) | 100 (1) | 10-1 (\(\dfrac{1}{10}\)) (0.1) | 10-2 (\(\dfrac{1}{100}\)) (0.01) | 10-3 (\(\dfrac{1}{1000}\)) (0.001) | 10-4 (\(\dfrac{1}{10000}\)) (0.0001) | ... |
| 2進数 | ... | 24 (16) 10000 | 23 (8) 1000 | 22 (4) 100 | 21 (2) 10 | 20 (1) 1 | 2-1 (\(\dfrac{1}{2}\)) (0.5) | 2-2 (\(\dfrac{1}{4}\)) (0.25) | 2-3 (\(\dfrac{1}{8}\)) (0.125) | 2-4 (\(\dfrac{1}{16}\)) (0.0625) | ... |
『イチ・ジュウ・ヒャク・セン・マン』と読まずに『イチ・ゼロ, イチ・ゼロ・ゼロ, ...』と読めばしっくりきます。
右シフトであふれるものは捨てられる
整数の右シフトではあるときから小数に変わります。10進数ではドット(.)をつければ0を左に追加して際限なく続けられますが、2進数では簡単にドットを付けれないので切り捨てられます。
また2進数では整数と小数は分けて考えます。用意される箱(変数)もちがう。(整数は固定。小数は浮動小数。)
\[1000 = 100 = 10 = 1\phantom{0} |ここから切り捨て→| = 0 = 0 \cdots\]
これが2進数の算術シフトのルールのひとつ。
右シフトで左に空いたところに符号ビットを入れる
算術シフトではもうひとつルールがあります。右シフトで左にできた空白に符号ビットを埋めること。
\begin{array}{l}
プラスの右シフト\\
01000 \rightarrow 00100 \rightarrow 00010 \rightarrow 00001\phantom{0} |ここから切り捨て| \rightarrow 00000 \rightarrow 00000 \cdots\\[10px]
マイナスの右シフト\\
11000 \rightarrow 11100 \rightarrow 11110 \rightarrow 11111\phantom{0} |ここから切り捨て| \rightarrow 11111 \rightarrow 11111 \cdots
\end{array}
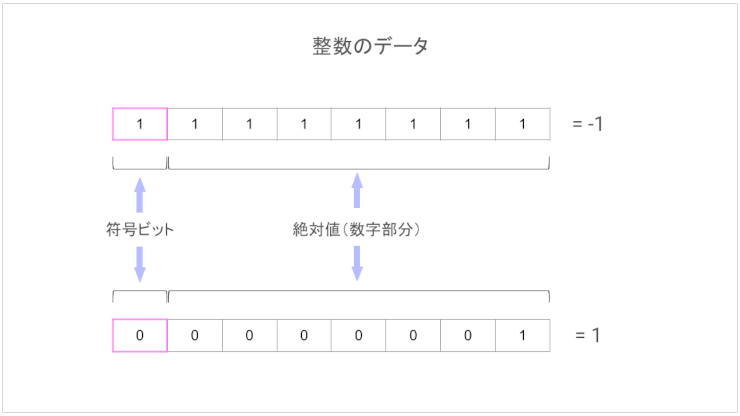
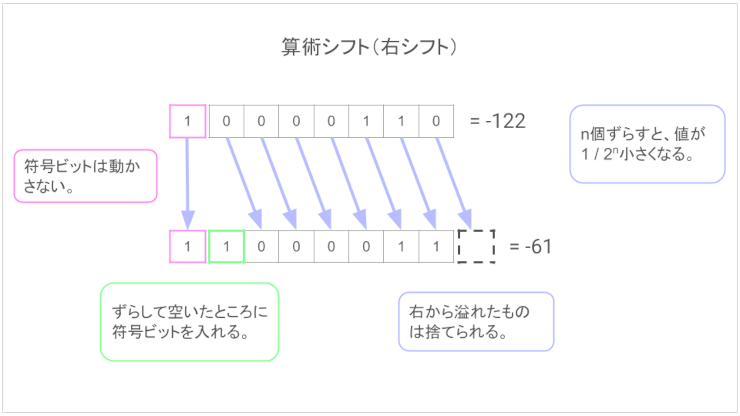
プラス値とマイナス値の絶対値が変わる正体。そりゃ、習った10進数 -> 2進数変換で答えが合いません。
なぜそんな面倒なことを?
マイナス値の算術シフト(右シフト)はなぜ0を埋めたらいけないんでしょうか?
ひとつは、10進数は0を付ける・消すの人間の手作業で際限なくできますが、コンピューターはそうはいきません。必ずサイズのある箱に入れなきゃいけないので有効桁が必要です。
人間の脳みそに情報量の限界はなく(本当はあるのかもしれないが。)、コンピューターはCPUという部品で限界があるので、限られた資源でマイナス値を表現しないといけない。
そしてもうひとつは、補数の考え方。
2進数の補数は『0と1を交代して+1)』でできちゃいます。このとき符号ビットも反転させる。
じつは10進数で補数を使った引き算は、一部が上手く行きません。昔のすごく頭のいい人が考えたので凡人にはそこまで説明できない。
2進数の絶対値は絶対値と言えるのか?
ここで小学生に戻ってみましょう。
プラス値は1, 2, 3, 4, ...と値が大きくなると数字も大きくなります。
でも、マイナス値は-1, -2, -3, -4, ...と値が小さくなると数字は大きくなります。
当たり前っちゃ当たり前なんですけど、この当たり前が2進数には通用しない。
絶対値は『基準0からの距離』のことで、中学校に入るとすぐXY軸の2次元グラフで習います。
コンピュータの内部で使う2進数のマイナス値の絶対値は、絶対値だけで10進数へ変換するととんでもない値になる。
ここが重要です。
一見すると0と1のコードだけ見れば絶対値とは言えませんが、2進数では『プラスとマイナスで絶対値のコードはちがうけど、絶対値として見ているよ?』ということ。
10進数に直せばきちんと絶対値が表示されます。
2進数整数の符号ビット以外の値の動き
ここで、2進数整数の数字の動きをまとめます。下の図は符号ビットを除いた値の部分。
| 2進値 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| そのまま 10進に変 換した値 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 実際の 10進値 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 2進値 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| そのまま 10進に変 換した値 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 実際の 10進値 | -16 | -15 | -14 | -13 | -12 | -11 | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 |
並べたら分かりますが、プラス値のコードをそのまま左にコピーして、マイナス符号を追加したものになります。
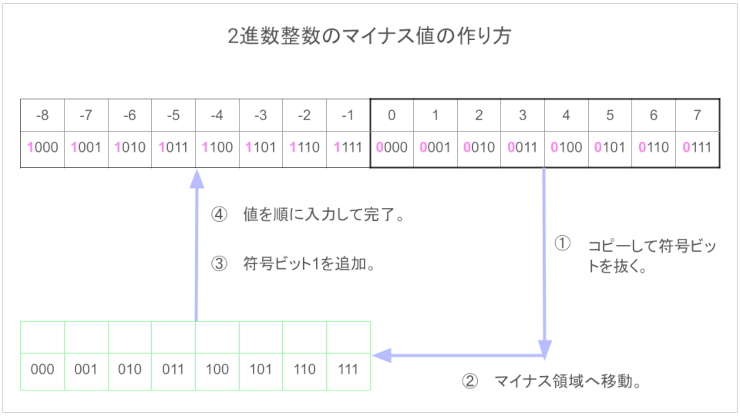
この図を覚えましょう。比較のために10進数の図も載せておきます。
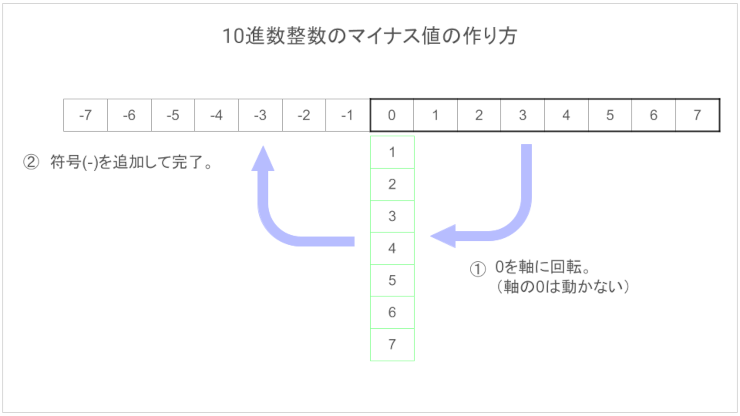
10進数では0を軸に数字の列をぐり~んと回転させるんですが2進数はそのまま。だから、絶対値が逆転して、マイナス値の大小と絶対値の大小が連動する。(値が小さくなると0に向かう。)
また、10進数は0が軸になるのでマイナスで使われず、2進数は0もマイナス値の最小値に使われるので1個多く表現できます。
このメカニズムのおかげで10進数⇔2進数の変換は『あるもの』でできます。ビックリするくらい簡単に。
マイナス値の10進数→2進数変換 = 補数
マイナス値の10進数から2進数への変換は、補数そのものです。
唐突すぎますね? 具体的に行きましょう。
2進数で出てくる補数は、引き算を足し算だけで実現するときに使います。
\[X - Y = X + (Yの補数)\]
まだ理解が微妙なら式を変えていきましょう。
\begin{array}{lll}
X-Y &=&X+(Yの補数)\\
X-Y\textcolor{#cf2e2e}{-X} &=&X+(Yの補数)\textcolor{#cf2e2e}{-X}\\
-Y &=&(Yの補数)
\end{array}
ここで冒頭に出てきた-9を使います。
\begin{array}{rcl}
9の2進数 &= &01001\\
9の補数 &= &10110 + 1 = 10111\\
Y &= &9\\[10px]
-Y &= &(Yの補数)\\
-9 &= &10111\\
\end{array}
方程式みたいの見せられたら眠くなるという人はこの図で覚えてください。
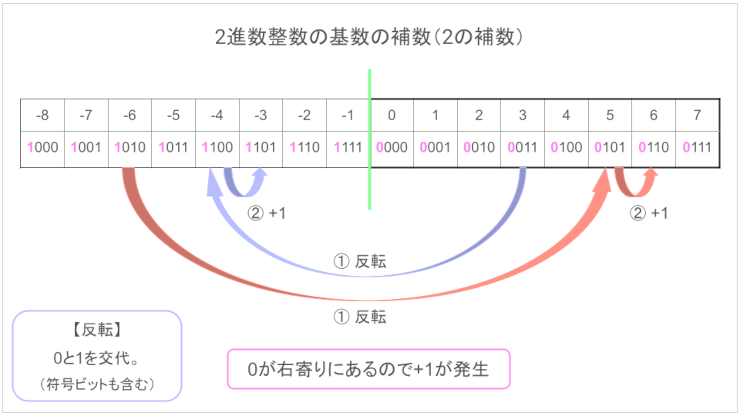
なぜ2進数は反転するのか? +1するのか? 分かると思います。
10進数は絶対値を0を中心に時計の針のように回すので符号を付け替えるだけでできるんですが、2進数はスライドさせてマイナス値を作っているので、プラマイの符号を変えるのはアウト。
そのスライドに合った方法が反転+1。プラス1はマイナス値に0を使っているのでその分ずれるから。
10進数の0は符号がありません。0自身がプラスとマイナス値のスタート地点だから。
でも2進数では、プラス用の0とマイナス用の0があります。それぞれ符号ビットだけで区別される。
| 正の0 | 0000 |
| 負の0 | 1000 (値は負の最小値) |
10進数でいう0は正の0。負の0は負の値の最小値に使われる。
反転とプラス1の順序は絶対に守る!
反転の前にプラス1はできないことに注意しましょう。
10進数では絶対値を+1すると正負のどちらも外に向かって動くので変わりませんが、2進数ではプラスは外、マイナスは内に動くので、まったく値が変わってしまいます。
図で言えば矢印の着地が変わってしまう。
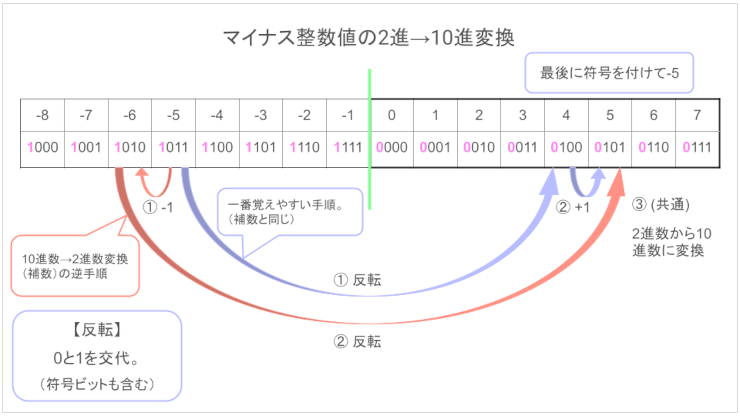
マイナス値の2進数→10進数変換は符号に気をつける
今度は、2進数から10進数へ変換するときです。このとき注意が必要なのは必ず最初に符号ビットを見ること。
プラスかマイナスで変換方法がまったくちがいます。
プラス値(符号ビットが0)ならそのまま変換していいです。
\begin{array}{rcl}
0101 &= &2^2\times1 + 2^1\times0+2^0\times1\\
&=&4\times1 + 2\times0 + 1\times1\\
&=&4 + 0 + 1\\
&=&5
\end{array}
マイナス値なら反転+1して符号(-)を付ける。
???と思った人もいるでしょう。マイナス値を10進数から2進数へ変換するとき補数を出せばいいと言いました。それと全く同じことして戻るの? と思ったはず。(最後に符号を付けることを除いて。)
百聞は一見にしかず。やってみましょう。
\[1011の反転+1:0100+0001 = 0101\]
\begin{array}{rcl}
0101 &= &2^2\times1 + 2^1\times0+2^0\times1\\
&=&4\times1 + 0 + 1\\
&=&4+1\\
&=&5
\end{array}
\[符号を付けて\underline{-5}\]
逆にすると面倒になる
本当にあってるか信じられないかもしれないので、面倒ですが10進→2進変換(補数)の逆手順でやってみます。
10進→2進の手順
(1) -○○の符号を抜いた〇〇の補数を考える。
(2) ○○を2進数に変換
(3) 2進数を反転
(3) 2進数を+1
2進→10進の手順(リバース)
(1) 2進数を-1
(2) 2進数を反転。
(2) 2進数を10進数に変換。(〇〇を出す。)
(3) 〇〇に符号(-)を付ける。
\begin{array}{l}
2進数を-1:1011-0001 = 1010\\
反転:0101
\end{array}
\begin{array}{rcl}
0101 &=&2^3\times0 + 2^2\times1 + 2^1\times0 + 2^0\times1\\
&= &0+4\times1 + 0 + 1\times1\\
&=&4+1\\
&=&5
\end{array}
\[符号を付けて\underline{-5}\]
式で証明するのは面倒ですが、図にすると一目瞭然です。