2進数から10進数へ変換するとき "1101" は "13" になるんですが、正確には不正解です。この答えはある条件下では○。
この変換結果は情報処理の試験ではよく見かけるんですが、じっさいのプログラミングではむしろ異例。プログラマーが最初に思い浮かべる答えは別にあります。
『プログラマーが思い浮かべる答え』を知らないまま話を進めると、モヤモヤして気持ち悪いのでいきなり答えから。
答えは "-5"。
マイナス値です。2進数では、プラス値(0を含む)とマイナス値では、0と1の並びのコードがある法則で異なります。
それが10進数とはちがうので、2進数から10進数に変換したときに値がまったく別物になります。
それを知らせてくれるのが符号ビット。だからタイトルで『符号ビットを見てますか?』と言ったんですね?
さっそく、符号ビットをみてどう判断するのか見てきましょう。今回は整数に限定します。小数は浮動小数を使ってまた別の話になるので。
今回は浮動小数に触れませんが、浮動小数には整数部というエリアがあり、その部分に関しては同じになります。
まず最初に一番左を見る
2進数では10進数のように符号(+, -)が使えません。数字の2~9が使えないようにコンピューターは0と1しか分からないから。
それは符号にも言えます。符号も0と1で表現します。
| 10進 | 2進 |
|---|---|
| + | 0 |
| - | 1 |
10進数で符号を一番左に付けるように2進数でも一番左に付けます。それが0か1になるので、となりの数字部分の一部に見えてしまう。
人間にどう見えるかはどうでもよくてコンピューターが分かればいい。コンピューターは『一番大きい位の値は符号』と認識します。
だから冒頭の "1101" は "-5" って言ってるんですね? プログラマーはコンピューターがどう思うかを想像するので、情報処理の試験とはちがう答えを出します。
| 符号 ビット | 絶対値(数字部分) |
|---|---|
| 1 | 0010111 |
符号ビットは省略できない
コンピューターは一番左の値を符号として見るので、そこに絶対値を入れることはできません。
(じっさいは入れる方法がある。それはあとで。)
冒頭で "1101" の "13" はまちがいと言いましたが、13の2進数が欲しければ "01101" です。人間からすれば一番左の0を付け忘れただけですが、コンピューターからすればまったくちがう。
\begin{array}{rcl}
13 &= &8+4+1\\
&=&(2^3\times\textcolor{#cf2e2e}{1}) + (2^2\times\textcolor{#cf2e2e}{1}) + (2^1\times\textcolor{#cf2e2e}{0}) + (2^0\times\textcolor{#cf2e2e}{1})\\[10px]
&\rightarrow &\underline{1101}
\end{array}
このように、10進数から2進数への変換で式を完成させて喜んで終わってしまいがちですが、必ず最後は0を付けましょう。
ちなみにマイナス値はこの変換方法が使えません。
符号を見たら変換方法を変える
2進数⇔10進数の変換をするとき、符号を見てプラスかマイナスが分かったら、それに合った変換方法を行います。
変換方法はプラスとマイナスではまったくちがう。それを頭に入れておくにはこの図を覚えておくといいです。
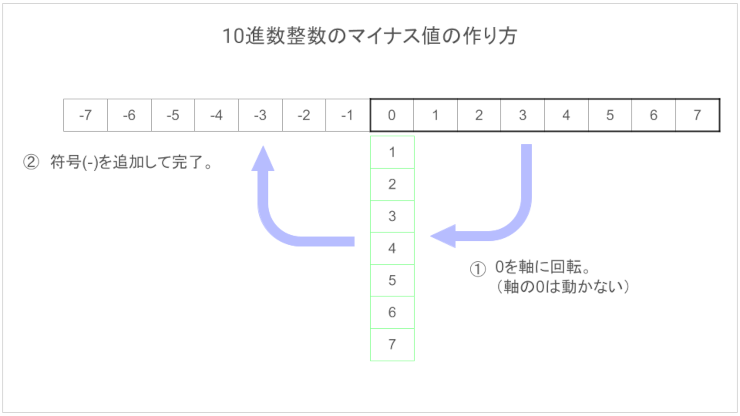
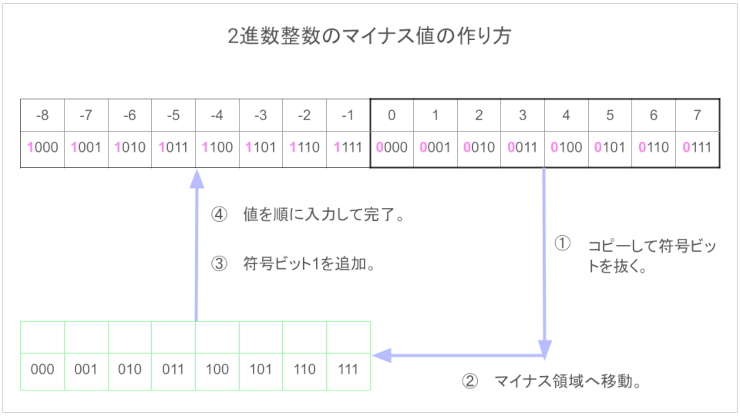
これに加えて算術シフトの考えも入ってくるのですが、くわしくはすでに書いたのでここではこの辺にしておきます。
プラス値の変換。教科書でよく見るもの。
プラス値の変換は、10進数⇔2進数の変換でよく見る方法を素直にするだけです。さっき出した式をもう一回出しときます。
\begin{array}{rcl}
13 &= &8+4+1\\
&=&(2^3\times\textcolor{#cf2e2e}{1}) + (2^2\times\textcolor{#cf2e2e}{1}) + (2^1\times\textcolor{#cf2e2e}{0}) + (2^0\times\textcolor{#cf2e2e}{1})\\[10px]
&\rightarrow &1101\\
&\rightarrow &\underline{01101}
\end{array}
これは10進数→2進数の変換。逆の2進数→10進数の変換はこれ。
\begin{array}{rcl}
01101\rightarrow 1101 &= &(2^3\times1) + (2^2\times1)+(2^1\times0)+(2^0\times1)\\
&=&(8\times1) + (4\times1) + (2\times0) + (1\times1)\\
&=&8 + 4 + 1\\
&=&\underline{13}
\end{array}
マイナス値の変換。反転して+1(補数を出す。)
マイナス値の変換のキーワードは『反転して+1』。10進数→2進数、2進数→10進数変換の両方ともです。
"-5"を使ってみていきましょう。10進数→2進数の変換はこうなります。まず、5の2進数を求めます。
\begin{array}{rcl}
5 &= &4+1\\
&=&(2^2\times\textcolor{#cf2e2e}{1}+(2^1\times\textcolor{#cf2e2e}{0})+(2^0\times\textcolor{#cf2e2e}{1})\\[10px]
&\rightarrow &101\\
&\rightarrow &\underline{0101}
\end{array}
次に『反転して+1』を考えます。『反転して+1』は補数(基数の補数, 2の補数)です。2進数の補数は、引き算を足し算にするものなのでこの式が成り立つ。
\begin{array}{rcl}
X - Y &= &X + (Yの補数)\\
(X -X) -Y &=& (X-X) +(Yの補数)\\[10px]
-Y &=& (Yの補数)
\end{array}
もうかんたんですね? Y = 5として式を進めていけば答えが出ます。
\begin{array}{rcl}
-5 &= &(5の補数)\rightarrow(2進数)\rightarrow(0101の補数)\\
&\rightarrow&(反転)\rightarrow1010\\
&\rightarrow&(+1)\rightarrow1010 + 0001 = \underline{1011}
\end{array}
今度は逆に2進数→10進数に変換します。まずは反転して+1をします。
\begin{array}{l}
1011&\rightarrow&(反転)\rightarrow0100\\
&\rightarrow&(+1)\rightarrow0100 + 0001 = \underline{0101}\\
\end{array}
これを10進数に変換して終わり。
\begin{array}{rcl}
0101 &= &(2^2\times\textcolor{#cf2e2e}{1}) + (2^1\times\textcolor{#cf2e2e}{0}) + (2^0\times\textcolor{#cf2e2e}{1})\\
&=&4 + 1\\
&=&\underline{5}
\end{array}
補数ってなんだ? 『反転して+1』がイマイチと言う人はこの図を覚えてください。
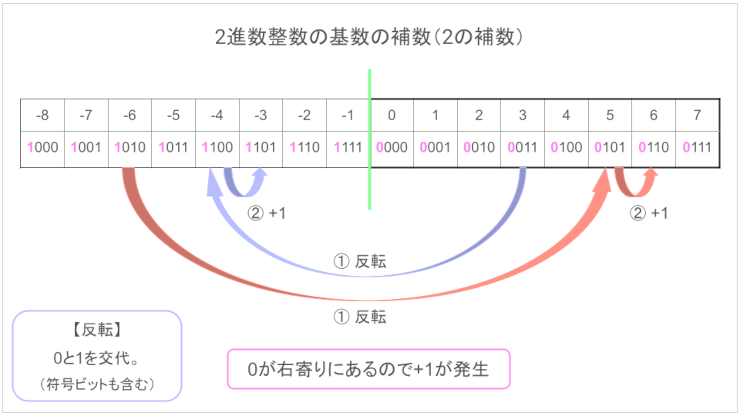
また、『なんで符号ビットごと反転するの?』と思うでしょう。くわしい解説はこちらでしています。
試験ではちゃんと問題を読む
ここまでの話で、あたかも情報処理の試験はまちがってると思われるように書いていますが、試験問題を見るとおそらくこう書いてあるはずです。
問○
次の正の整数の...
試験ではよく使われる『他教科の試験で国語力が試される』の典型。数学など数式を解くときに重要な条件が隠されています。
(じっさいは隠れてない。見落としてるだけ。)
この『正の』がないのに符号ビットを無視した表記は指摘していいレベル。その問いは配点が無効になって全員○になるでしょう。
まぁ、出てくる2進数の一番左がぜんぶ0だったら『あってもなくても答えは同じだよね?』と言われて返り討ちにあうけど。
正の整数を明示して表現範囲を約2倍に
2進数では有効数字の桁数が必ず決まります。符号ビットが一番左にあるので、残りの数字の個数が有効桁。
でもこれだと、正の整数しか使わないとき約半分は無駄になる。
| 符号 ビット | 絶対値 (0000~1111) |
| 0 | 0~15 |
| 1 | -16~-1 (これがいらない。) |
そんなときは『符号ビットは数値の最大桁として見てください。』と命令することができます。そうすると表現範囲は約2倍になる。
| 絶対値 (00000~11111) |
| 0~31 |
この命令はプログラミングで行います。たとえばC/C++ならこうなる。
| 変数型 | サイズ | 表現範囲 |
|---|---|---|
| char | 1byte (8bit) | -128 ~ 127 |
| unsigned char | 1byte (8bit) | 0 ~ 255 |
| int | 4byte (32bit) | -2,147,483,648 ~ 2,147,483,647 |
| unsigned int | 4byte (32bit) | 0 ~ 4,294,967,295 |
un + signedは(サイン(符号)をアン(否定)する)という意味。












