普段使う整数値(10進数)で、000876とは書いたりしません。左の0は意味がないもので876だからです。
これが有効数字や有効桁数(有効数字の桁数)の考え方です。
でも2進数では110と0110はまったくちがいます。10進数に変換すると値が変わる。じつは符号(+,-)もちがう。ここが2進数のポイント。
2進数の勉強をしていると100や0100を10進数変換してこんな答えを出すと思います。
\begin{array}{rrrr}
110 = &2^{2}\times1 + 2^{1}\times1+2^{0}\times0 = &4 + 2 + 0= &6\\
0110 = &2^{3}\times0 +2^{2}\times1 + 2^{1}\times1+2^{0}\times0 = &0 + 4 + 2+ 0= &6
\end{array}
確かに2進数から10進数への変換はまちがっていないんですが、実際の値はこうなります。
\begin{array}{rrr}
110 &= &-2\\
0110 &= &6
\end{array}
符号も違うし絶対値も変わってまったく別物。なぜこうなるの?という話です。
今回は有効数字や有効桁の話でもあるんですが、小数点の話はせず整数に限定します。小数点は浮動小数点などまた別の話になるので。
2進数は符号も0と1
符号は一番左に付けます。10進数では+と-を使いプラスが省略できます。
\begin{array}{r}
-2\\
+6\\
6\\
\end{array}
2進数も一番左に付けるのところまでは同じですが、符号は使えません。コンピューターは0と1しか分からないので+, -の記号を付けても意味が分かりません。
符号も0と1で表現します。符号ビットと言います。
| 符号 | 符号 ビット |
|---|---|
| + | 0 |
| - | 1 |
110が-2になってしまうのは、一番大きい位の値を『5』とせず、符号として見ているから。
正符号(+)も付けてもらわないと最大の位の値なのか符号なのか分かりません。だから2進数では符号ビット0も省略できません。
これで、\(110=-2\)と\(0110=6\)になる理由が分かりましたね?
2進数では正符号を省略できない。符号ビットを必ず付ける。
2進数の符号ビットはひとつじゃない
これだけではありません。次の2進数→10進数の変換を見てください。
\begin{array}{r}
010\rightarrow2\\
0010\rightarrow2\\
00000010\rightarrow2
\end{array}
これは分かりますね? さっきの変換方法で導けます。それならこれはどうでしょう?
\begin{array}{r}
110\rightarrow-2\\
1110\rightarrow-2\\
11111110\rightarrow-2
\end{array}
そんなバカな!と思うかもしれませんが、こうなります。もちろん、さっきの変換方法では出せない。これが2進数のマイナス整数の中身です。
空いたところに符号ビットを埋める算術シフト
2進数整数は算術シフトを使います。算術シフトのルールでは、空いた左のビットに符号ビットを埋めることになっています。
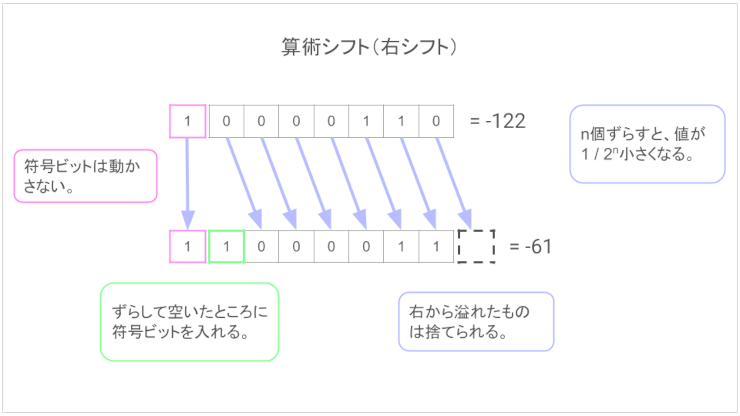
『2進数の符号ビットはひとつじゃない』と言ったのはこういうことなんですが、じっさい符号として見ているのは一番左だけです。
あくまで符号ビットはひとつだけ。
『符号を埋めたところを値にすると、10進数にしたとき値がめちゃくちゃ変わるじゃないか?』と思うでしょうが、それでも上手くいくようになっています。
2進数のマイナス整数の表現はちょっと特殊です。話が長くなるのでくわしくはこちらを見てください。
有効数字を省略する10進数
10進数の有効数字、有効桁は中学校で習った気がしますが整数部分ではありません。整数の有効桁になると高校数学(たぶん)の指数表現になります。
義務教育では整数部分の有効桁は意識しません。
たとえば、『123』と『82』の有効桁は?とか問われません。答えは『3と2』です。それなら『123 + 82』の82の有効桁はどうなるでしょうか?
答えは『3』。足し算の結果も含めて最大の有効桁に合わせるから。
10進数の整数の有効桁は暗黙の了解です。人間のさじ加減でいくらでも桁を上げて書くことができるのでわざわざ明示しません。
最初に『082とか書かない』と言ったのはそういうこと。
値をバッサリ切る有効桁
学校の数学では有効数字と近似値は同時に教えるはずです。近似値は数値を切の良いところで無視すること。
四捨五入が一般的です。というか学校教育では近似値の出し方 = 四捨五入が暗黙の了解になっている。
(ときおり切り捨てもあるが。)
どこで切るかの基準が有効数字、その桁数が有効桁。
小数点については習ってるので誰でもできますが、じつは整数にもあります。有効桁が2桁という条件なら次の簡単な足し算の結果はこうなる。
\begin{array}{r}
56\\[-3px]
\underline{+\phantom{0}78}\\[-3px]
34
\end{array}
有効数字、有効桁の『有効』は『値として有効』『値を切っても正しい』という意味。
円周率を3.14にしているのは、円に見えるなら、計算上問題ないなら、これ以上細かい円周率じゃなくていいってこと。
もちろん、精密な工業製品や科学技術の分野になると、もっと細かい数字じゃないとダメってことになります。
そのときは有効数字、有効桁が変わる。
学校ではなく、社会で使われる有効数字、有効桁はもっとシビアです。
工業製品などの有効桁は、製品としてきちんと成立する値にする。具体的には壊れない、組み立てたときにズレがない値。
完成品として問題ない、無視できる値が捨てられる。
科学技術はもっとシビア。最近、アメリカや中国は火星や月など宇宙にアグレッシブですが、これらの世界はもっと細かい数値が必要。寸分のズレも許さないということ。
寸分といってもどこかで切りますが。
一時期、学校教育で円周率を3で計算しても良いみたいな話(ある意味でガセだった)がありましたが、納得してた人は子どもに教える資格ない。
円周率3は正六角形です。円ではありません。また、円周率を4にすると正方形です。
『.14』は有効数字なので、円であるために重要です。いかなる理由でも消していいなんてありえません。
もう20年も前の話で、今はそんなことしてないので安心してください。
有効数字の意味を知らないと、たとえガセでもこういうことになっちゃいます。
有効数字を省略できない2進数。切り捨てがデフォルト
2進数では、必ず符号ビットを付けるので、有効数字、有効桁が決まります。さっきのマイナスの2進数をもう一度見てみましょう。
\begin{array}{r}
110\rightarrow-2\\
1110\rightarrow-2\\
11111110\rightarrow-2
\end{array}
なんですべてが-2なのかもう分かりますね?これらは有効数字が2で有効桁がそれぞれ、2, 3, 7だから -2 です。
(符号ビットは数に入れない。)
もうひとつ、有効数字と有効桁のちがいも分かります。
有効数字は数値として有効な桁数(ここでは2)、有効桁は表現する数値のサイズです。
コンピューターは勝手にサイズ(桁)を変えられない
2進数では値を切るのに四捨五入を使いません。明示しないかぎり切り捨てです。コンピューターは人間とちがって自由に桁(サイズ)を変えられないから。
サイズが自由だとメモリやCPUがパンクします。プログラマが指定した桁数を超えるとその分の値は切り捨てられます。
これを桁あふれ(オーバーフロー)と言います。
オーバーフローの切り捨ては一番大きい位でも起きるので、値がとんでもないことになります。さっきの足し算で100が捨てられように。
ここを調整するのが人間(プログラマ)の仕事です。
丸める・丸め誤差とオーバーフロー
ちなみに、値をバッサリ切る行為を『丸める』といい、そこで発生する誤差のことを『丸め誤差』といいます。
四捨五入や切り捨ては丸める方法のことを指す。
桁あふれも丸め誤差なんですが、若干使い方のニュアンスにちがいがあります。
| オーバーフロー | 有効桁がまちがって起きるもの。 プログラマのミスが原因の場合が多い。 人間のミスで悪い意味で使う。 |
| 丸め誤差 | 丸める方法に都合が悪くて値が変わるもの。 浮動小数点ではどうしても起こるものがある。 現象を指す。 |
丸める・丸め誤差は小数でよく出てくる。
2進数整数の有効数字はアバウトなものじゃない
ここの説明で最初は、このような文章を入れようと思いました。
10進数でいう『1.00』『1.000』『1.0000000』みたいなもの。
しかしあることに気づいてすぐに止めました。
\begin{array}{ccccccl}
1.00 &= &1.000 &= &1.0000000&\leftarrow&間違い\\
1.00 &\neq &1.000 &\neq &1.0000000 &\leftarrow&正解\\
1.00 &\fallingdotseq &1.000 &\fallingdotseq &1.0000000 &\leftarrow&正解\\
\end{array}
1.00は『1.001かもしれない』『1.001259かもしれない』。ニアイコールはそういう意味。
1.001や1.001259かもしれないけど、とりあえず1.00としましょう。ということ。
2進数では『かもしれない』はありません。表現範囲(桁)にある0と1の羅列で必ず値が決まります。
有効数字・有効桁をはっきりさせるのは、この『かもしれない』を無くすことです。
まぁ、整数の話をしているのに小数を出すのはどうかと思ったのもあるけど。10進数でも整数には『かもしれない』はほとんど使わないし。